H2 Essay Title
Authors
Prime Intellect Team
February 10, 2026

Introducing Lab: The Full-Stack Platform for Training your Own Models

Today, we are launching Lab.

Built from the ground up for agentic post-training, Lab unifies the Environments Hub with Hosted Training and Hosted Evaluations into a full-stack platform for research and model optimization.

Our platform enables the entire lifecycle of post-training research — from large-scale agentic RL, to inference and evaluation — without needing to worry about the costs of massive GPU clusters or the headaches of low-level algorithm details.

Giving everyone their own frontier AI lab.

Last year, we launched the Environments Hub, a place for anyone to build and share RL environments and evals. Since then, over 1k+ unique environments have been created by 250+ creators, with more than 100k total environment downloads.

Today, we’re taking the next step in our mission to make frontier infrastructure, currently locked behind the walls of big labs, accessible to any researcher, engineer or company.

Over the past few weeks in private beta, more than 3,000 RL runs have been completed by individuals and companies around the world. Starting today, we’re opening it up to everyone.

If you are an AI company, you can now be your own AI lab.

If you are an AI engineer, you can now be an AI researcher.

Why this matters: Model ↔ Product Optimization Loop

The current zeitgeist believes a few big labs will automate all knowledge work, own the intelligence layer, and control the future direction of AI.

We don't find this future inspiring, nor do we think it's inevitable.

We believe in the decade of agents, where taking models the “last mile” across all verticals of the economy will be a very arduous process, and will require a continuous feedback loop between the real world; Tesla autopilot is a good analogy here, where the iteration cycle between deployment and model improvements took years to get it ready for full autonomy.

The same story will play out for agentic models.

The big labs realize this, they need you to teach their models how to integrate into your workforce and workflows. They need you to do the last-mile work with skills, scaffolds, and prompts. But they're not giving you the tools you need. They're adamant about owning the intelligence layer, owning the optimization loop, and closing off their models behind a black box.

As long as you depend on their closed APIs and closed models, you don't have sovereignty over your intelligence. While they're doing everything they can to convince you to build on their models, despite telling everyone they’d steamroll them, and wanting to gain full control over the future of AI, we are taking the complete opposite approach.

We give you full control and ownership over your models. We don't want you locked into our APIs, we're not asking you to share your reasoning traces, and we don't want to accumulate all the money and compute. We want you to build your own models, control your own intelligence, and have a stake in the superintelligence buildout — so we can collectively shape the future of AI we want to exist.

We want a free and open market of creators, startups and companies to outcompete the big labs in every vertical, and have full ownership in the upside in the process. This is not just a missionary plan, but it’s also a winning strategy.

‍

If you think of models as just a form of software, the best way to integrate your software into as many systems as possible is through open-source. This story has played out countless times, with Linux being perhaps the canonical example, where its adaptability, extensibility, and security embedded it across the software stack. Open models, and open frameworks for building and deploying agents will achieve the same.

This same story played out with AOL versus the open Internet. AOL tightly controlled which applications you could access through their platform. Then browsers created an open platform where anyone could build anything. The collective creativity of an open ecosystem created better apps than AOL ever could, quickly won over users, and ultimately enabled some of the most valuable companies of today.

‍

—

We believe that granting full control over the model to product optimization loop can enable a similar outcome for AI.

There's a reason breakthrough products like ChatGPT and Claude Code were created by the labs themselves — they have access to the full model optimization loop, something that isn't possible for teams building purely on APIs.

If every company had the same access to frontier training infrastructure, the collective creativity of the market would unlock far more breakthroughs.

We’re already starting to see enterprises and application-layer AI startups realize this. Cursor is beginning to post-train their own models optimized directly for Cursor itself as the RL environment, to gain more sovereignty over their product stack.

We want more application-layer companies entering the training game for every vertical of the economy.

‍

We are the Bazaar to the big lab Cathedrals.

Lab is our attempt to pave the path towards a different future from the one you’ve been sold.

One where the skills to shape intelligence are available to everyone, not constrained to a select few.
One where every AI company can be their own AI lab, and every AI engineer can be an AI researcher.
One where a free and open market collectively shapes the future direction of AI.
One where AI is open and decentralized.

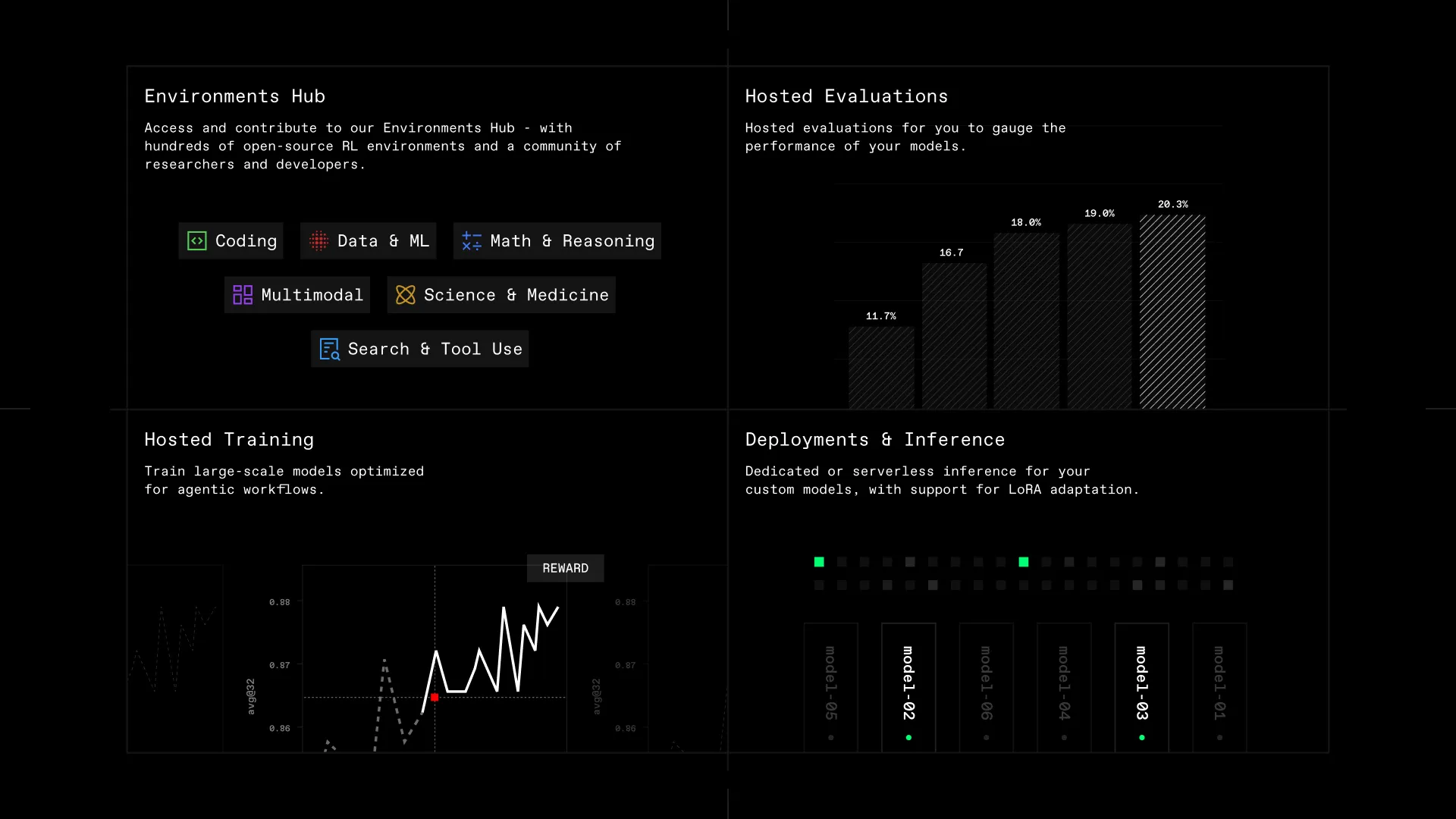
Product — The Prime Intellect Lab

The Prime Intellect Lab enables the entire lifecycle of post-training research; from large-scale agentic RL, to inference and evaluation, without needing to worry about the costs of massive GPU clusters or the headaches of low-level algorithm details. It unifies the Environments Hub with Hosted Training and Hosted Evaluations into a full-stack platform for research and optimization.

Lab is built around environments, which contain everything needed to run a model on your task:

  • A dataset of tasks
  • A harness for the model (tools, sandboxes, context management, etc.)
  • A rubric to score the model's performance

Use environments to train models with reinforcement learning, evaluate capabilities, generate synthetic data, optimize prompts, experiment with agent harnesses, and more.

Getting Started with Lab

prime lab setup

Similar to many web app frameworks, where running a single setup command prepares an opinionated project structure, you can run prime lab setup and be off to the races for your own AI lab, with a full workspace prepared for you to be able to fire up your coding agent of choice, ask any questions, get the right answers, and adhere to best practices for development and research experiments.

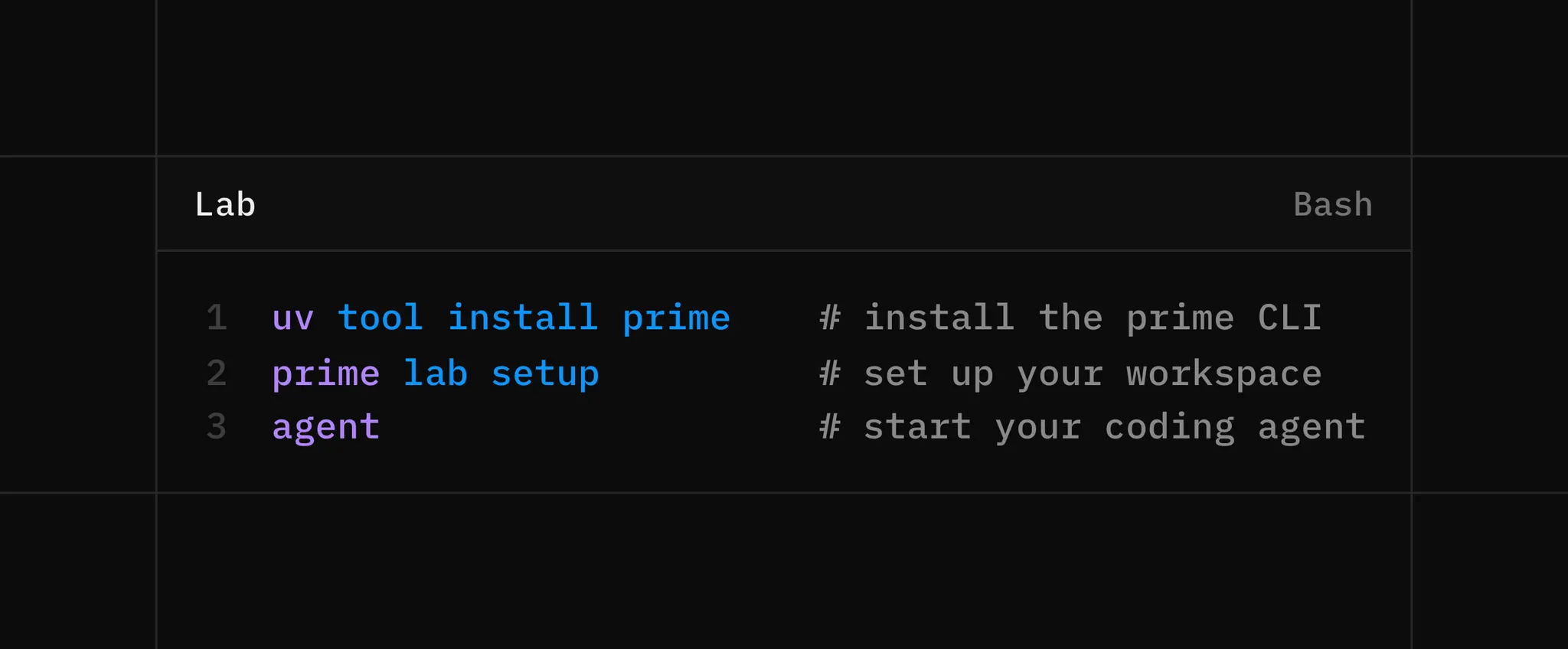
Once your workspace is set up, you can launch your first training run

Hosted Training

Hosted Training allows you to run large-scale training experiments in your own environments without worrying about the infrastructure. We’re launching with support for agentic RL with LoRA, built atop our prime-rl training library. We’ll be adding support for SFT and other algorithms (e.g. GEPA, GKD, DPO) in the near future.

‍

Configuring a Run

To see the list of currently available models for Hosted Training, do:

‍

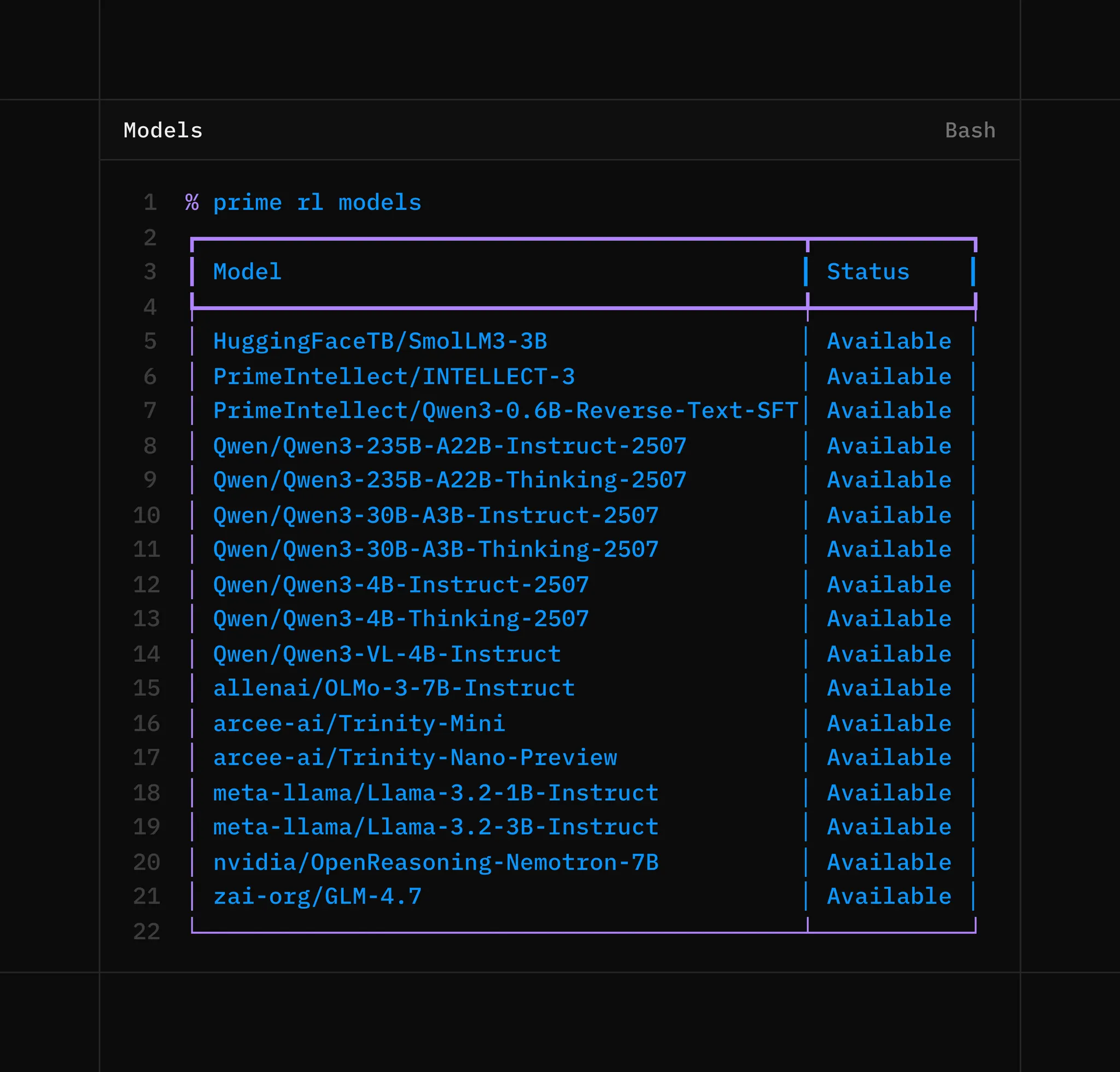
Beyond our own INTELLECT-3 model, many awesome small and large models are available from organizations such as Nvidia, Arcee, Hugging Face, Allen AI, Z.AI, Alibaba Qwen, and many more launching soon.

We’ve also added experimental multimodality support and have deployed our first models to train on environments with image input.

Runs are configured via a simple .toml file:

# configs/lab/alphabet-sort.toml
model = "Qwen/Qwen3-30B-A3B-Instruct-2507"
max_steps = 100
batch_size = 512
rollouts_per_example = 16

[sampling]
max_tokens = 512

[[env]]
id = "primeintellect/alphabet-sort"       # Environments Hub ID

To start a training, run:

prime rl run configs/alphabet-sort.toml

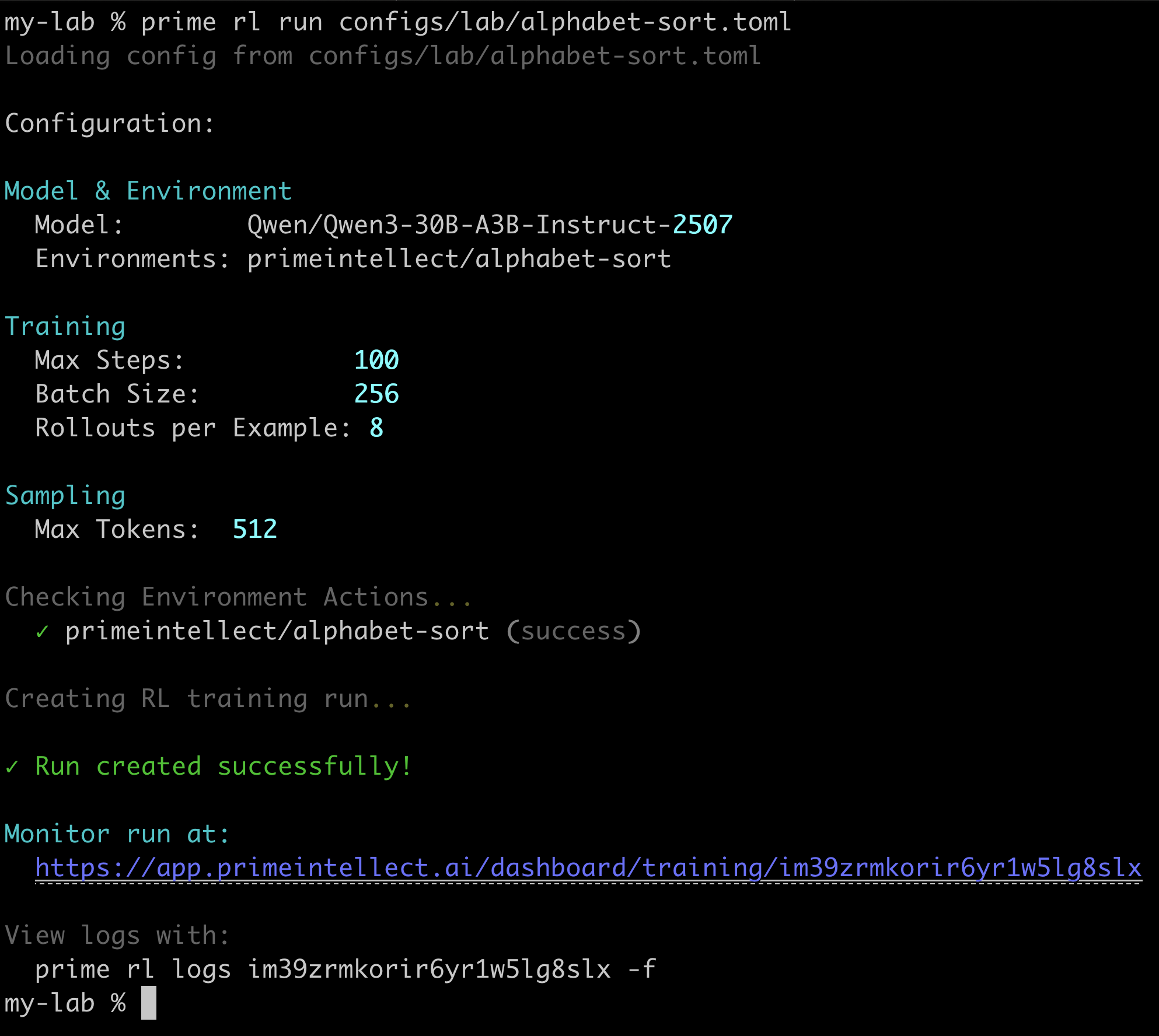
You can then view logs, training results, and rollouts via the Lab platform, or completely agent-native in your terminal.

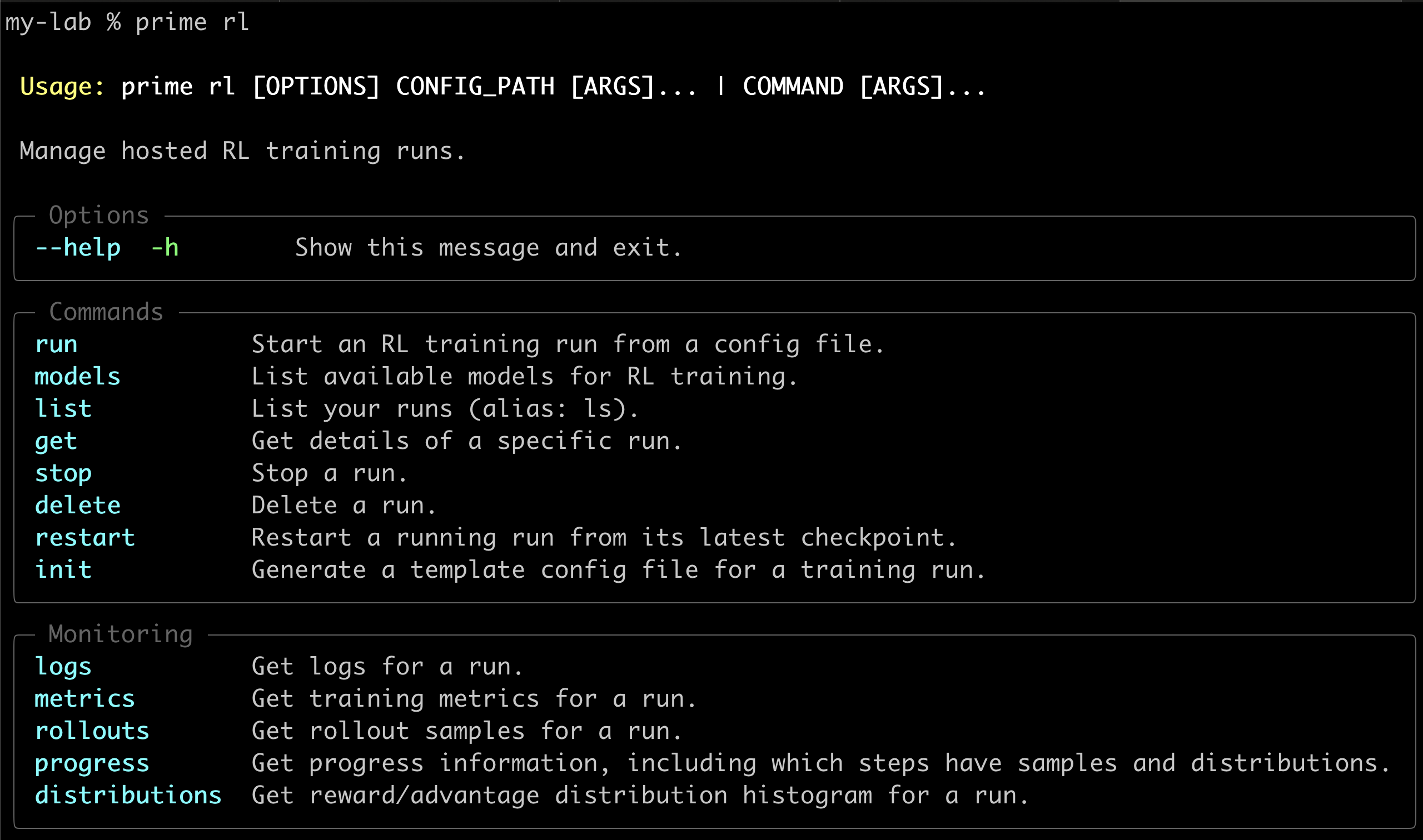
For full Lab documentation, our hosted training platform, including running evaluations, deploying models for production, and more, go here.

Infrastructure

Lab makes use of the same underlying infrastructure we’ve built for training open frontier models. This includes our async RL trainer prime-rl, verifiers, the Environments Hub, sandboxes for secure code execution, and hosted evaluations.

Hosted Training

Hosted training builds upon prime-rl - our framework for large-scale asynchronous reinforcement learning.

How it Works

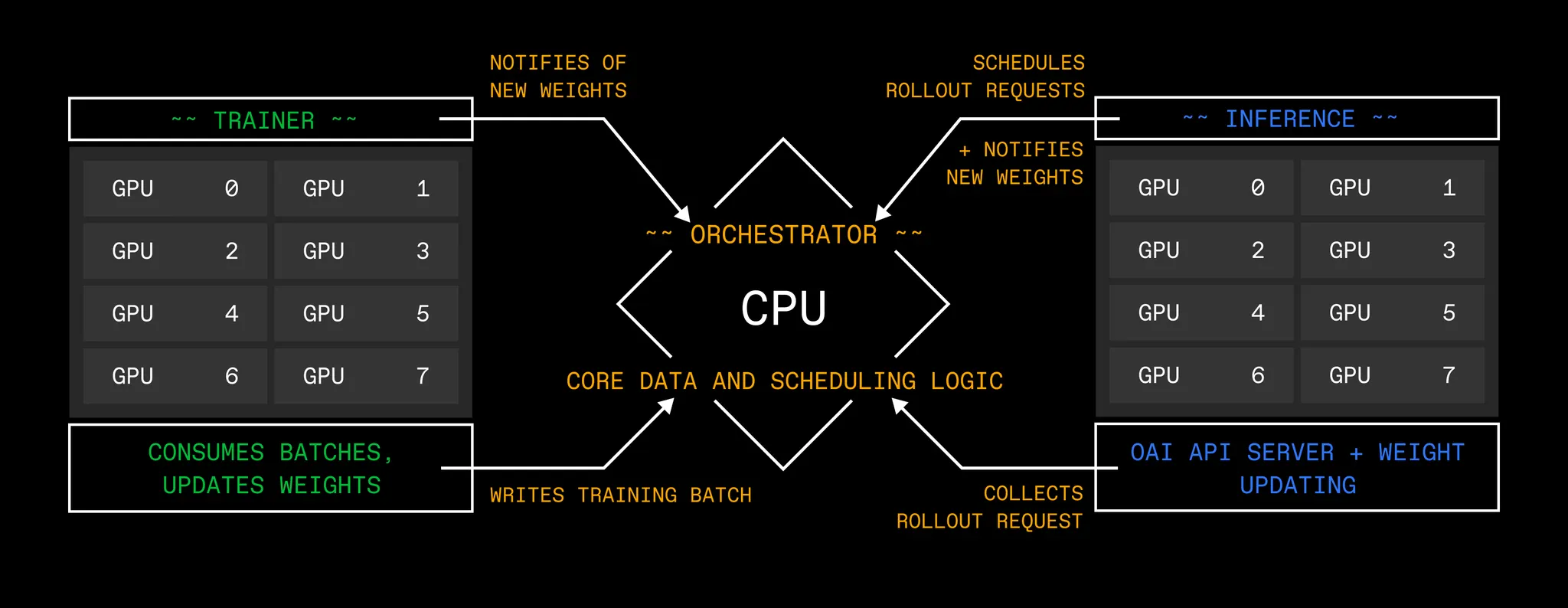
The 3 key components of the prime-rl architecture are the Trainer, Inference, and the Orchestrator.

For Hosted Training, each run is allocated to a dedicated Orchestrator which manages environment logic, and we manage multi-tenant LoRA deployments for the Trainer and Inference. This allows shared hardware across runs, enabling high efficiency and per-token pricing.

Deployment

The most interesting AI use cases require models with state of the art capabilities. However, running dedicated, fine-tuned deployments of large Mixture of Experts models per customer is infeasible and wasteful. Instead, for the production inference on our Lab platform, we use multi-tenant LoRA inference deployments with customized models built on the Nvidia Dynamo stack.

Learn more about how to deploy production inference for your fine-tuned model in the docs.

Next steps

This is just the beginning. Lab will serve as our platform to productionize all our research initiatives and make them accessible to anyone. We want Lab to become the default platform for doing AI research, and to broaden access to the tools to optimize models.

Over the coming weeks and months, we will be shipping SFT support, dedicated deployments for full fine-tuning, online distillation, and much more.

Beyond that, we will place ambitious bets at the frontier of where the puck is going and build infrastructure for the problems we believe are most consequential, such as:

  • Long-horizon agents and our work on recursive language models (RLMs)
  • Online RL and continual learning - The future is models that learn in production. Training and inference collapse into a single, continuous loop - This fundamentally changes infrastructure requirements. Our stack was designed for this world via a tight integration between rollout, training, and serving.
  • Specialization and behaviour shaping
  • Automated AI research and science

Q&A

Join the PI discord to discuss, share feedback, and ask any questions

‍

Eurus-2-PRIME
System Prompt
When tackling complex reasoning tasks, you have access to the following actions. Use them as needed to progress through your thought process. [ASSESS] [ADVANCE] [VERIFY] [SIMPLIFY] [SYNTHESIZE] [PIVOT] [OUTPUT] You should strictly follow the format below: [ACTION NAME] # Your action step 1 # Your action step 2 # Your action step 3 ... Next action: [NEXT ACTION NAME]
User
Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients $2$ and $-2,$ respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53).$ Find $P(0) + Q(0).$
Eurus-2-PRIME
[ASSESS]

We are given two quadratic polynomials $P(x)$ and $Q(x)$ with leading coefficients $2$ and $-2$, respectively. The graphs of both polynomials pass through the points $(16,54)$ and $(20,53)$. We need to find the value of $P(0) + Q(0)$.

[ADVANCE]

Let's express the quadratic polynomials $P(x)$ and $Q(x)$ in the general form:
$ P(x) = 2x^2 + bx + c $
$ Q(x) = -2x^2 + dx + e $

Since the graphs of both polynomials pass through the points $(16,54)$ and $(20,53)$, we can substitute these points into the equations of $P(x)$ and $Q(x)$ to form a system of equations.

For $P(x)$:
$ P(16) = 2(16)^2 + 16b + c = 54 $
$ 512 + 16b + c = 54 $
$ 16b + c = -458 \quad \text{(Equation 1)} $

$ P(20) = 2(20)^2 + 20b + c = 53 $
$ 800 + 20b + c = 53 $
$ 20b + c = -747 \quad \text{(Equation 2)} $

For $Q(x)$:
$ Q(16) = -2(16)^2 + 16d + e = 54 $
$ -512 + 16d + e = 54 $
$ 16d + e = 566 \quad \text{(Equation 3)} $

$ Q(20) = -2(20)^2 + 20d + e = 53 $
$ -800 + 20d + e = 53 $
$ 20d + e = 853 \quad \text{(Equation 4)} $

[ADVANCE]

Now, we can solve the system of equations for $P(x)$:
Subtract Equation 1 from Equation 2:
$ (20b + c) - (16b + c) = -747 - (-458) $
$ 4b = -289 $
$ b = -\frac{289}{4} $

Substitute $b = -\frac{289}{4}$ into Equation 1:
$ 16\left(-\frac{289}{4}\right) + c = -458 $
$ -1156 + c = -458 $
$ c = 698 $

So, for $P(x)$, we have:
$ P(x) = 2x^2 - \frac{289}{4}x + 698 $
$ P(0) = 698 $

Next, we can solve the system of equations for $Q(x)$:
Subtract Equation 3 from Equation 4:
$ (20d + e) - (16d + e) = 853 - 566 $
$ 4d = 287 $
$ d = \frac{287}{4} $

Substitute $d = \frac{287}{4}$ into Equation 3:
$ 16\left(\frac{287}{4}\right) + e = 566 $
$ 1148 + e = 566 $
$ e = -582 $

So, for $Q(x)$, we have:
$ Q(x) = -2x^2 + \frac{287}{4}x - 582 $
$ Q(0) = -582 $

[ADVANCE]

Finally, we can find $P(0) + Q(0)$:
$ P(0) + Q(0) = 698 + (-582) = 116 $

So, the value of $P(0) + Q(0)$ is $\boxed{116}$.
INTELLECT-MATH-7B-SFT (ours)
System Prompt
Solve the following math problem efficiently and clearly. Think carefully and step by step about your response and reason before providing a final response. Conclude your response with: \n\nTherefore, the final answer is: $\\boxed{answer}$. I hope it is correct.\n\nWhere [answer] is just the final number or expression that solves the problem.
User
Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients $2$ and $-2,$ respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53).$ Find $P(0) + Q(0).$
INTELLECT-MATH-7B-SFT
So I've got this problem here about quadratic polynomials $P(x)$ and $Q(x)$. $P(x)$ has a leading coefficient of $2$, and $Q(x)$ has a leading coefficient of $-2$. Both polynomials pass through the points $(16,54)$ and $(20,53)$. I need to find $P(0) + Q(0)$.

First, since both $P(x)$ and $Q(x)$ are quadratic polynomials, I can express them in the general form:

$P(x) = 2x^2 + bx + c$

$Q(x) = -2x^2 + dx + e$

Wait, actually, the leading coefficient is the coefficient of the highest power of $x$, which for a quadratic is $x^2$. So yes, $P(x) = 2x^2 + bx + c$ and $Q(x) = -2x^2 + dx + e$.

Now, both polynomials pass through the points $(16,54)$ and $(20,53)$. That means when $x=16$, $P(16)=54$, and when $x=20$, $P(20)=53$. Similarly for $Q(x)$.

So, I can set up equations using these points.

First, for $P(x)$:

$P(16) = 2(16)^2 + b16 + c = 54$

Similarly, $P(20) = 2(20)^2 + b20 + c = 53$

Let me calculate $16^2$ and $20^2$:

$16^2 = 256$

$20^2 = 400$

So,

$P(16): 2256 + 16b + c = 54 \Rightarrow 512 + 16b + c = 54 \Rightarrow 16b + c = 54 - 512 \Rightarrow 16b + c = -458$

$P(20): 2400 + 20b + c = 53 \Rightarrow 800 + 20b + c = 53 \Rightarrow 20b + c = 53 - 800 \Rightarrow 20b + c = -747$

Now, I have two equations:

1) $16b + c = -458$

2) $20b + c = -747$

I can subtract equation 1 from equation 2 to eliminate $c$:

$(20b + c) - (16b + c) = -747 - (-458)$

$20b + c - 16b - c = -747 + 458$

$4b = -289$

So, $b = -289 / 4 = -72.25$

Wait, but coefficients are usually integers, but maybe not. Let me check.

Now, plug $b$ back into one of the equations to find $c$. Let's use equation 1:

$16(-72.25) + c = -458$

$-1156 + c = -458$

$c = -458 + 1156 = 698$

So, $P(x) = 2x^2 - 72.25x + 698$

Hmm, $P(0)$ would be $c$, which is $698$.

Now, let's do the same for $Q(x)$.

$Q(16) = -2*(16)^2 + d16 + e = 54 \Rightarrow -2256 + 16d + e = 54 \Rightarrow -512 + 16d + e = 54 \Rightarrow 16d + e = 54 + 512 \Rightarrow 16d + e = 566$

$Q(20) = -2*(20)^2 + d20 + e = 53 \Rightarrow -2400 + 20d + e = 53 \Rightarrow -800 + 20d + e = 53 \Rightarrow 20d + e = 53 + 800 \Rightarrow 20d + e = 853$

Now, equations for $Q(x)$:

1) $16d + e = 566$

2) $20d + e = 853$

Subtract equation 1 from equation 2:

$(20d + e) - (16d + e) = 853 - 566$

$4d = 287$

$d = 287 / 4 = 71.75$

Now, plug $d$ back into equation 1:

$1671.75 + e = 566 \Rightarrow 1148 + e = 566 \Rightarrow e = 566 - 1148 = -582$

So, $Q(x) = -2x^2 + 71.75x - 582$

Therefore, $Q(0) = e = -582$

Now, $P(0) + Q(0) = 698 + (-582) = 116$

Wait, but the problem says "present the answer in LaTeX format: \boxed{Your answer}"

So, I should write $\boxed{116}$

But let me double-check my calculations to make sure I didn't make any mistakes.

First, for $P(x)$:

$P(16) = 2(256) + 16b + c = 512 + 16b + c = 54 \Rightarrow 16b + c = -458$

$P(20) = 2*(400) + 20b + c = 800 + 20b + c = 53 \Rightarrow 20b + c = -747$

Subtracting: $4b = -289 \Rightarrow b = -72.25$

Then, $c = -458 - 16*(-72.25) = -458 + 1156 = 698$

Similarly for $Q(x)$:

$Q(16) = -2*(256) + 16d + e = -512 + 16d + e = 54 \Rightarrow 16d + e = 566$

$Q(20) = -2*(400) + 20d + e = -800 + 20d + e = 53 \Rightarrow 20d + e = 853$

Subtracting: $4d = 287 \Rightarrow d = 71.75$

Then, $e = 566 - 16*71.75 = 566 - 1148 = -582$

So, $P(0) = 698$, $Q(0) = -582$, sum is $116$.

Seems correct.

Final Answer

$\boxed{116}$
INTELLECT-MATH-7B (ours)
System Prompt
Solve the following math problem efficiently and clearly. Think carefully and step by step about your response and reason before providing a final response. Conclude your response with: \n\nTherefore, the final answer is: $\\boxed{answer}$. I hope it is correct.\n\nWhere [answer] is just the final number or expression that solves the problem.
User
Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients $2$ and $-2,$ respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53).$ Find $P(0) + Q(0).$
INTELLECT-MATH-7B
So I have two quadratic polynomials, $P(x)$ and $Q(x)$, with leading coefficients 2 and -2, respectively. Both pass through the points $(16,54)$ and $(20,53)$. I need to find $P(0) + Q(0)$.

First, since both are quadratic polynomials, I can express them in the general form:

$P(x) = 2x² + bx + c$

$Q(x) = -2x² + dx + e$

But since both pass through the points $(16,54)$ and $(20,53)$, I can set up equations using these points.

For $P(x)$:

$P(16) = 2*(16)² + b \cdot 16 + c = 54$

$P(20) = 2(20)² + b \cdot 20 + c = 53$

Similarly for $Q(x)$:

$Q(16) = -2(16)² + d \cdot 16 + e = 54$

$Q(20) = -2(20)² + d \cdot 20 + e = 53$

Let's compute the squares:

$16² = 256$

$20² = 400$

So for $P(x)$:

$2256 + 16b + c = 54 \Rightarrow 512 + 16b + c = 54 \Rightarrow 16b + c = 54 - 512 = -458 \quad ...(1)$

$2400 + 20b + c = 53 \Rightarrow 800 + 20b + c = 53 \Rightarrow 20b + c = 53 - 800 = -747 \quad ...(2)$

For $Q(x)$:

$-2256 + 16d + e = 54 \Rightarrow -512 + 16d + e = 54 \Rightarrow 16d + e = 54 + 512 = 566 \quad ...(3)$

$-2400 + 20d + e = 53 \Rightarrow -800 + 20d + e = 53 \Rightarrow 20d + e = 53 + 800 = 853 \quad ...(4)$

Now, I have two systems of linear equations:

For $P(x)$:

$16b + c = -458 \quad ...(1)$

$20b + c = -747 \quad ...(2)$

Subtract equation (1) from equation (2):

$(20b + c) - (16b + c) = -747 - (-458)$

$4b = -289 \Rightarrow b = -\frac{289}{4}$

Now plug $b$ back into equation (1):

$16\left(-\frac{289}{4}\right) + c = -458 \Rightarrow -1156 + c = -458 \Rightarrow c = -458 + 1156 = 698$

So $P(x) = 2x² - \frac{289}{4}x + 698$

For $Q(x)$:

$16d + e = 566 \quad ...(3)$

$20d + e = 853 \quad ...(4)$

Subtract equation (3) from equation (4):

$(20d + e) - (16d + e) = 853 - 566$

$4d = 287 \Rightarrow d = \frac{287}{4}$

Now plug $d$ back into equation (3):

$16\left(\frac{287}{4}\right) + e = 566 \Rightarrow 1148 + e = 566 \Rightarrow e = 566 -1148= -582$

So $Q(x)=-2x^{2}+\frac{287}{4}x-582$.

Now, $P(0)=c=698$.

$Q(0)=e=-582$.

Therefore, $P(0)+Q(0)=698+(-582)=116$.

Final Answer

$\boxed{116}$.
Authors
Prime Intellect Team
Share
Acknowledgements

Recursive Language Models: the paradigm of 2026

A blueprint for “context folding”: recursively compressing and reshaping an agent’s own context to prevent context rot and keep ultra-long, multi-step rollouts cheap and reliable without relying solely on external file-based scaffolding.

January 1, 2026

INTELLECT-3: A 100B+ MoE trained with large-scale RL

Today, we release INTELLECT-3, a 100B+ parameter Mixture-of-Experts model trained on our RL stack, achieving state-of-the-art performance for its size across math, code, science and reasoning benchmarks, outperforming many larger frontier models.

November 26, 2025

Scaling Our Open-Source Environments Program

Today, we're scaling up our open-source environments program to become the global hub for open evals and RL environments.As part of this, we're committing hundreds of thousands of $ in grants and looking for partners who want to join our mission to accelerate open superintelligence.

October 27, 2025

ESSAYS

Related Posts

Recursive Language Models: the paradigm of 2026

A blueprint for “context folding”: recursively compressing and reshaping an agent’s own context to prevent context rot and keep ultra-long, multi-step rollouts cheap and reliable without relying solely on external file-based scaffolding.

January 1, 2026

INTELLECT-3: A 100B+ MoE trained with large-scale RL

Today, we release INTELLECT-3, a 100B+ parameter Mixture-of-Experts model trained on our RL stack, achieving state-of-the-art performance for its size across math, code, science and reasoning benchmarks, outperforming many larger frontier models.

November 26, 2025

Scaling Our Open-Source Environments Program

Today, we're scaling up our open-source environments program to become the global hub for open evals and RL environments.As part of this, we're committing hundreds of thousands of $ in grants and looking for partners who want to join our mission to accelerate open superintelligence.

October 27, 2025