H2 Essay Title
Authors
Prime Intellect Team
Announcements
August 27, 2025

Environments Hub: A Community Hub To Scale RL To Open AGI

RL environments are the playgrounds where agents learn. Until now, they’ve been fragmented, closed, and hard to share. We are launching the Environments Hub to change that: an open, community-powered platform that gives environments a true home.

Environments define the world, rules and feedback loop of state, action and reward.  From games to coding tasks to dialogue, they’re the contexts where AI learns, without them, RL is just an algorithm with nothing to act on.

Environments sit at the center of current AI progress. Each new one expands what we can train, study, and evaluate, making open models more competitive. By lowering the friction to build, share, and reuse environments, the Hub enables anyone in the world to contribute directly to open-source AGI progress.

In last week’s private beta, over 30 researchers and companies contributed environments to the Hub. Starting today, we’re opening it up to everyone - building the open alternative to the closed research tooling of big labs, with infra for RL, Reinforcement Fine-tuning (RFT), compute, and inference. We want to ensure that the next wave of startups, AI progress and adoption is built on open rails and open models, and not fed into the walled gardens of big labs, ultimately entrenching their lead.

Motivation

Most current discussion around RL environments centers on a wave of startups whose business model is to build and sell them exclusively to a handful of large closed labs.

This trend poses both a serious risk and an opportunity. If high-quality environments remain expensive and closed, open-source models will fall further behind. But if a robust ecosystem of open-source environments and training tools emerges, open-source can set the state of the art.

Right now, open research lacks the tools to study many of the questions big labs consider most critical. With this release, we aim to change that. The Environment Hub, together with the RL infrastructure we’re building around it, is designed to enable the next wave of startups and AI progress to be built on open rails and open models.

Next Steps: Providing The Full-Stack Open AGI Infrastructure

In the last months, we’ve made significant progress scaling agentic RL training to the largest open model sizes. With many crowdsourced environments feeding into INTELLECT-3, we are confident we can train a fully open, state-of-the-art agentic model.

Beyond INTELLECT-3, our focus with the Environments Hub is on making this infrastructure accessible to everyone: enabling researchers and startups alike to train models for their own tasks, integrate tools, run Reinforcement Fine-Tuning (RFT), and optimize agent scaffolds. Our entire stack is open-source (prime-rl), and we are extending it to run seamlessly on top of our global compute supply.

We believe RL is not only the path to AGI, but also the foundation for building AI-native products. The most successful future startups will emerge by creating novel and differentiated environments tailored to their needs. Today, the biggest barrier is not access to models - trillion-parameter agentic models already exist - but the infrastructure and cost of training and serving them at scale. By lowering this barrier, we aim to give any AI builder cheap, seamless access to compute, inference, and training, along with the full RL infrastructure stack, which is currently locked behind the walls of closed labs.

If you’re excited to help shape the future of a truly sovereign open-source AI ecosystem, we’d love to hear from you and invite researchers and companies to:

  • Contribute: Develop environments & evals for the Environments Hub. Get Started
  • Collaborate: We’re hiring engineers and researchers at the intersection of AI and distributed systems. Careers

‍

Quick Links

‍

Features

Developing and Sharing Environments

Create, manage and share environments for reinforcement learning and evaluation on the Environments Hub:

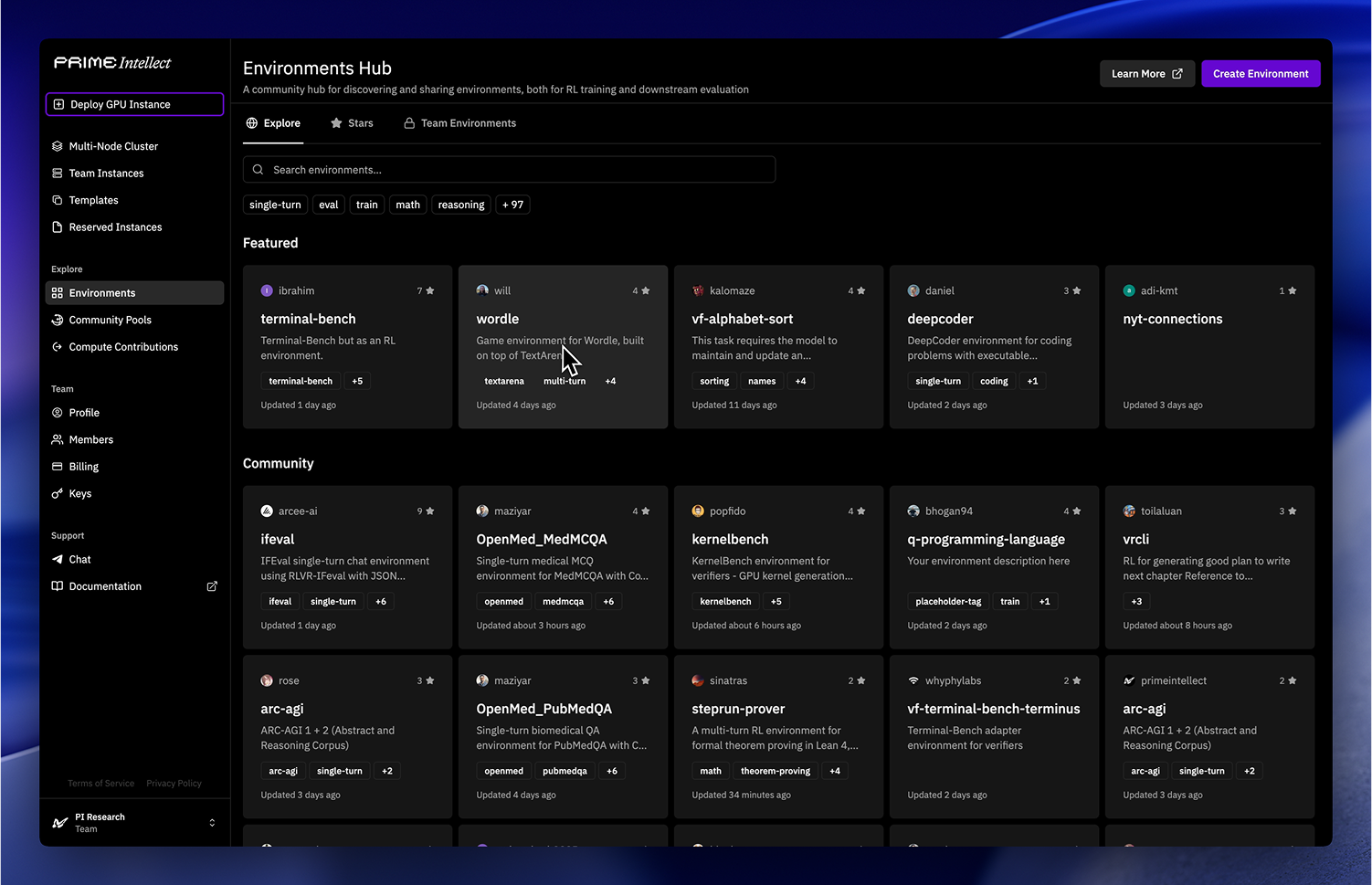
Evals

Create and explore evaluation reports for environments for various models.

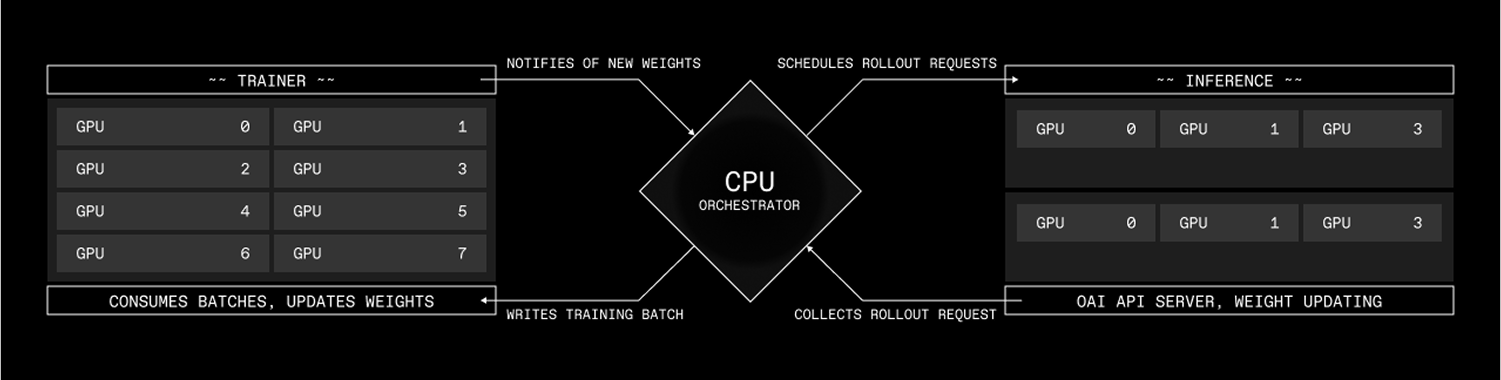
RL Training

Environments are natively supported in our scalable https://github.com/PrimeIntellect-ai/prime-rl trainer.

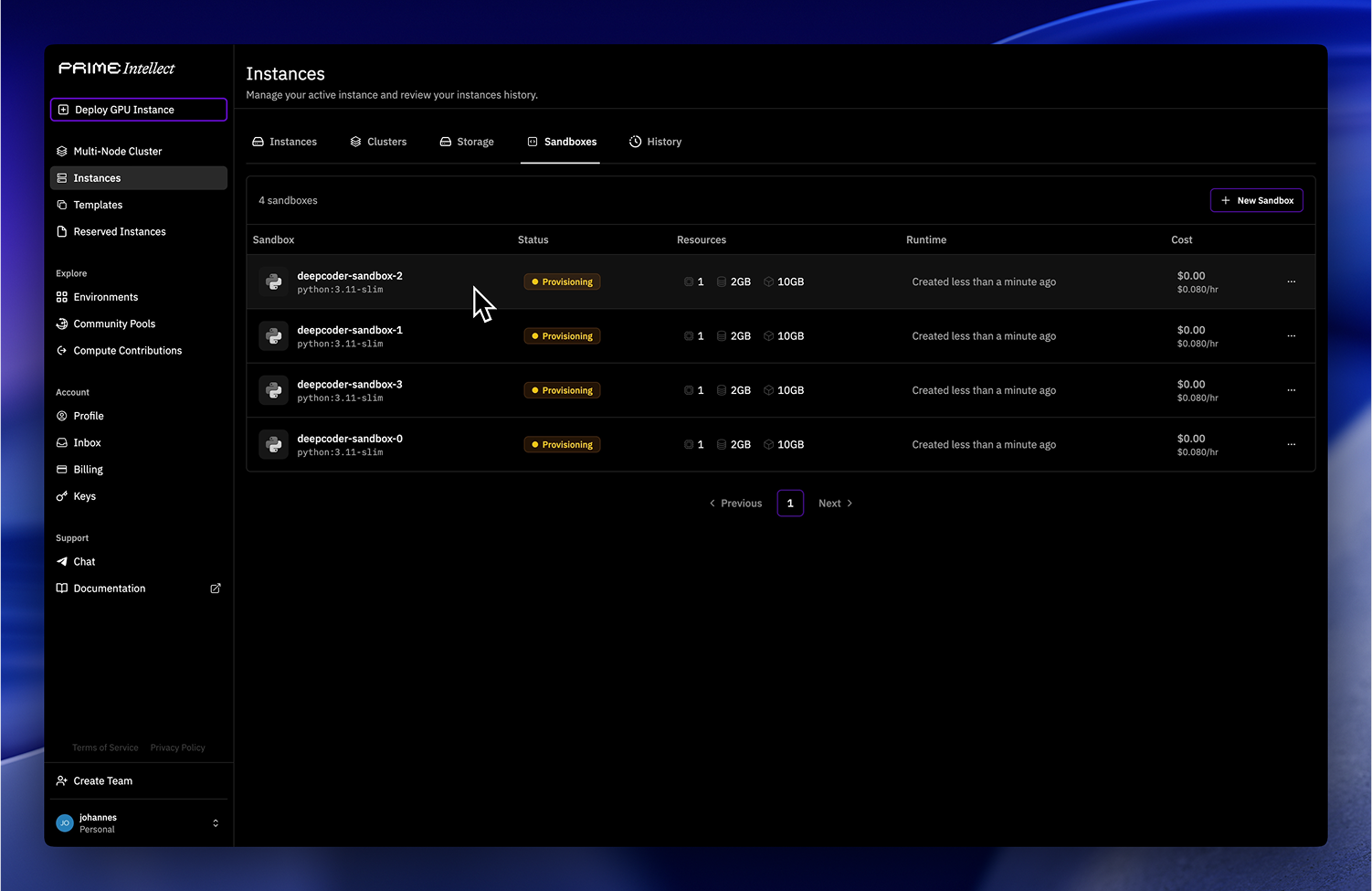
Sandboxes

We’re also launching sandboxes in beta that plug directly into Verifier Environments for secure code execution.

Contributors

A big thank you to all contributors during last week’s beta. Special shoutout to Arcee AI, Hud.so, WhyPhy Labs, Groq, and the many individuals who contributed their first environments to the hub!

With this launch, we’re also opening up a list of open and in-progress RFCs and bounties here. The tasks we’re sourcing are intentional. We want to collectively build towards a state-of-the-art open INTELLECT-3 model in agentic and coding tasks.

Let us know if you'd like to claim a lock on one (via an initial draft PR / design doc) by messaging Will or Johannes on X or opening a PR to https://github.com/PrimeIntellect-ai/prime-environments.

If you are interested in RL environments that don't have a bounty figure listed yet, just ask and we'll figure something out based on the difficulty scale we're using.

We are also opening up applications for novel environments and evals. Researchers accepted in this program will receive compute for running experiments, a stipend and support from our internal research team. Some moonshot examples of environments and evals we’d be especially excited about:

  • Robust code-quality evaluations for agentic software engineering
  • Evaluating usage of filesystems and memory for long-running tasks
  • Adaptive coherent instruction-following for realistic multi-turn interactions
  • High-quality creative writing and style adherence
  • Generative generalist reward models with process critiques
  • Harness and task design for interactive data science + machine learning, such as:
    • Environments for NanoGPT speedrun optimizations
    • Terminal-friendly data visualization
    • Research plan generation, with recent notable papers as golden targets

Next Steps: Providing Full-Stack AGI Infrastructure

In the last months, we’ve made significant progress scaling agentic RL training to the largest open model sizes. With many crowdsourced environments feeding into INTELLECT-3, we are confident we can train a fully open, state-of-the-art agentic model.

Beyond INTELLECT-3, our focus with the Environments Hub is on making this infrastructure accessible to everyone: enabling researchers and startups alike to train models for their own tasks, integrate tools, run Reinforcement Fine-Tuning (RFT), and optimize agent scaffolds. Our entire stack is open-source (prime-rl), and we are extending it to run seamlessly on top of our global compute supply.

We believe RL is not only the path to AGI, but also the foundation for building AI-native products. The most successful future startups will emerge by creating novel and differentiated environments tailored to their needs. Today, the biggest barrier is not access to models - trillion-parameter agentic models already exist - but the infrastructure and cost of training and serving them at scale. By lowering this barrier, we aim to give any AI builder cheap, seamless access to compute, inference, and training and the full stack rl infrastructure, unlocking more full stack AI startups and builders.

Our goal is to provide every researcher and company with access to an open RL infrastructure stack - currently locked behind the walls of closed labs.

If you’re excited to help shape the future of a truly sovereign open-source AI ecosystem, we’d love to hear from you and invite researchers and companies to:

  • Contribute: Develop environments & evals for the Environments Hub. Get Started
  • Collaborate: We’re hiring engineers and researchers at the intersection of AI and distributed systems. Careers

Q&A

Join the PI discord to discuss, share feedback, and ask any questions :)

‍

Eurus-2-PRIME
System Prompt
When tackling complex reasoning tasks, you have access to the following actions. Use them as needed to progress through your thought process. [ASSESS] [ADVANCE] [VERIFY] [SIMPLIFY] [SYNTHESIZE] [PIVOT] [OUTPUT] You should strictly follow the format below: [ACTION NAME] # Your action step 1 # Your action step 2 # Your action step 3 ... Next action: [NEXT ACTION NAME]
User
Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients $2$ and $-2,$ respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53).$ Find $P(0) + Q(0).$
Eurus-2-PRIME
[ASSESS]

We are given two quadratic polynomials $P(x)$ and $Q(x)$ with leading coefficients $2$ and $-2$, respectively. The graphs of both polynomials pass through the points $(16,54)$ and $(20,53)$. We need to find the value of $P(0) + Q(0)$.

[ADVANCE]

Let's express the quadratic polynomials $P(x)$ and $Q(x)$ in the general form:
$ P(x) = 2x^2 + bx + c $
$ Q(x) = -2x^2 + dx + e $

Since the graphs of both polynomials pass through the points $(16,54)$ and $(20,53)$, we can substitute these points into the equations of $P(x)$ and $Q(x)$ to form a system of equations.

For $P(x)$:
$ P(16) = 2(16)^2 + 16b + c = 54 $
$ 512 + 16b + c = 54 $
$ 16b + c = -458 \quad \text{(Equation 1)} $

$ P(20) = 2(20)^2 + 20b + c = 53 $
$ 800 + 20b + c = 53 $
$ 20b + c = -747 \quad \text{(Equation 2)} $

For $Q(x)$:
$ Q(16) = -2(16)^2 + 16d + e = 54 $
$ -512 + 16d + e = 54 $
$ 16d + e = 566 \quad \text{(Equation 3)} $

$ Q(20) = -2(20)^2 + 20d + e = 53 $
$ -800 + 20d + e = 53 $
$ 20d + e = 853 \quad \text{(Equation 4)} $

[ADVANCE]

Now, we can solve the system of equations for $P(x)$:
Subtract Equation 1 from Equation 2:
$ (20b + c) - (16b + c) = -747 - (-458) $
$ 4b = -289 $
$ b = -\frac{289}{4} $

Substitute $b = -\frac{289}{4}$ into Equation 1:
$ 16\left(-\frac{289}{4}\right) + c = -458 $
$ -1156 + c = -458 $
$ c = 698 $

So, for $P(x)$, we have:
$ P(x) = 2x^2 - \frac{289}{4}x + 698 $
$ P(0) = 698 $

Next, we can solve the system of equations for $Q(x)$:
Subtract Equation 3 from Equation 4:
$ (20d + e) - (16d + e) = 853 - 566 $
$ 4d = 287 $
$ d = \frac{287}{4} $

Substitute $d = \frac{287}{4}$ into Equation 3:
$ 16\left(\frac{287}{4}\right) + e = 566 $
$ 1148 + e = 566 $
$ e = -582 $

So, for $Q(x)$, we have:
$ Q(x) = -2x^2 + \frac{287}{4}x - 582 $
$ Q(0) = -582 $

[ADVANCE]

Finally, we can find $P(0) + Q(0)$:
$ P(0) + Q(0) = 698 + (-582) = 116 $

So, the value of $P(0) + Q(0)$ is $\boxed{116}$.
INTELLECT-MATH-7B-SFT (ours)
System Prompt
Solve the following math problem efficiently and clearly. Think carefully and step by step about your response and reason before providing a final response. Conclude your response with: \n\nTherefore, the final answer is: $\\boxed{answer}$. I hope it is correct.\n\nWhere [answer] is just the final number or expression that solves the problem.
User
Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients $2$ and $-2,$ respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53).$ Find $P(0) + Q(0).$
INTELLECT-MATH-7B-SFT
So I've got this problem here about quadratic polynomials $P(x)$ and $Q(x)$. $P(x)$ has a leading coefficient of $2$, and $Q(x)$ has a leading coefficient of $-2$. Both polynomials pass through the points $(16,54)$ and $(20,53)$. I need to find $P(0) + Q(0)$.

First, since both $P(x)$ and $Q(x)$ are quadratic polynomials, I can express them in the general form:

$P(x) = 2x^2 + bx + c$

$Q(x) = -2x^2 + dx + e$

Wait, actually, the leading coefficient is the coefficient of the highest power of $x$, which for a quadratic is $x^2$. So yes, $P(x) = 2x^2 + bx + c$ and $Q(x) = -2x^2 + dx + e$.

Now, both polynomials pass through the points $(16,54)$ and $(20,53)$. That means when $x=16$, $P(16)=54$, and when $x=20$, $P(20)=53$. Similarly for $Q(x)$.

So, I can set up equations using these points.

First, for $P(x)$:

$P(16) = 2(16)^2 + b16 + c = 54$

Similarly, $P(20) = 2(20)^2 + b20 + c = 53$

Let me calculate $16^2$ and $20^2$:

$16^2 = 256$

$20^2 = 400$

So,

$P(16): 2256 + 16b + c = 54 \Rightarrow 512 + 16b + c = 54 \Rightarrow 16b + c = 54 - 512 \Rightarrow 16b + c = -458$

$P(20): 2400 + 20b + c = 53 \Rightarrow 800 + 20b + c = 53 \Rightarrow 20b + c = 53 - 800 \Rightarrow 20b + c = -747$

Now, I have two equations:

1) $16b + c = -458$

2) $20b + c = -747$

I can subtract equation 1 from equation 2 to eliminate $c$:

$(20b + c) - (16b + c) = -747 - (-458)$

$20b + c - 16b - c = -747 + 458$

$4b = -289$

So, $b = -289 / 4 = -72.25$

Wait, but coefficients are usually integers, but maybe not. Let me check.

Now, plug $b$ back into one of the equations to find $c$. Let's use equation 1:

$16(-72.25) + c = -458$

$-1156 + c = -458$

$c = -458 + 1156 = 698$

So, $P(x) = 2x^2 - 72.25x + 698$

Hmm, $P(0)$ would be $c$, which is $698$.

Now, let's do the same for $Q(x)$.

$Q(16) = -2*(16)^2 + d16 + e = 54 \Rightarrow -2256 + 16d + e = 54 \Rightarrow -512 + 16d + e = 54 \Rightarrow 16d + e = 54 + 512 \Rightarrow 16d + e = 566$

$Q(20) = -2*(20)^2 + d20 + e = 53 \Rightarrow -2400 + 20d + e = 53 \Rightarrow -800 + 20d + e = 53 \Rightarrow 20d + e = 53 + 800 \Rightarrow 20d + e = 853$

Now, equations for $Q(x)$:

1) $16d + e = 566$

2) $20d + e = 853$

Subtract equation 1 from equation 2:

$(20d + e) - (16d + e) = 853 - 566$

$4d = 287$

$d = 287 / 4 = 71.75$

Now, plug $d$ back into equation 1:

$1671.75 + e = 566 \Rightarrow 1148 + e = 566 \Rightarrow e = 566 - 1148 = -582$

So, $Q(x) = -2x^2 + 71.75x - 582$

Therefore, $Q(0) = e = -582$

Now, $P(0) + Q(0) = 698 + (-582) = 116$

Wait, but the problem says "present the answer in LaTeX format: \boxed{Your answer}"

So, I should write $\boxed{116}$

But let me double-check my calculations to make sure I didn't make any mistakes.

First, for $P(x)$:

$P(16) = 2(256) + 16b + c = 512 + 16b + c = 54 \Rightarrow 16b + c = -458$

$P(20) = 2*(400) + 20b + c = 800 + 20b + c = 53 \Rightarrow 20b + c = -747$

Subtracting: $4b = -289 \Rightarrow b = -72.25$

Then, $c = -458 - 16*(-72.25) = -458 + 1156 = 698$

Similarly for $Q(x)$:

$Q(16) = -2*(256) + 16d + e = -512 + 16d + e = 54 \Rightarrow 16d + e = 566$

$Q(20) = -2*(400) + 20d + e = -800 + 20d + e = 53 \Rightarrow 20d + e = 853$

Subtracting: $4d = 287 \Rightarrow d = 71.75$

Then, $e = 566 - 16*71.75 = 566 - 1148 = -582$

So, $P(0) = 698$, $Q(0) = -582$, sum is $116$.

Seems correct.

Final Answer

$\boxed{116}$
INTELLECT-MATH-7B (ours)
System Prompt
Solve the following math problem efficiently and clearly. Think carefully and step by step about your response and reason before providing a final response. Conclude your response with: \n\nTherefore, the final answer is: $\\boxed{answer}$. I hope it is correct.\n\nWhere [answer] is just the final number or expression that solves the problem.
User
Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients $2$ and $-2,$ respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53).$ Find $P(0) + Q(0).$
INTELLECT-MATH-7B
So I have two quadratic polynomials, $P(x)$ and $Q(x)$, with leading coefficients 2 and -2, respectively. Both pass through the points $(16,54)$ and $(20,53)$. I need to find $P(0) + Q(0)$.

First, since both are quadratic polynomials, I can express them in the general form:

$P(x) = 2x² + bx + c$

$Q(x) = -2x² + dx + e$

But since both pass through the points $(16,54)$ and $(20,53)$, I can set up equations using these points.

For $P(x)$:

$P(16) = 2*(16)² + b \cdot 16 + c = 54$

$P(20) = 2(20)² + b \cdot 20 + c = 53$

Similarly for $Q(x)$:

$Q(16) = -2(16)² + d \cdot 16 + e = 54$

$Q(20) = -2(20)² + d \cdot 20 + e = 53$

Let's compute the squares:

$16² = 256$

$20² = 400$

So for $P(x)$:

$2256 + 16b + c = 54 \Rightarrow 512 + 16b + c = 54 \Rightarrow 16b + c = 54 - 512 = -458 \quad ...(1)$

$2400 + 20b + c = 53 \Rightarrow 800 + 20b + c = 53 \Rightarrow 20b + c = 53 - 800 = -747 \quad ...(2)$

For $Q(x)$:

$-2256 + 16d + e = 54 \Rightarrow -512 + 16d + e = 54 \Rightarrow 16d + e = 54 + 512 = 566 \quad ...(3)$

$-2400 + 20d + e = 53 \Rightarrow -800 + 20d + e = 53 \Rightarrow 20d + e = 53 + 800 = 853 \quad ...(4)$

Now, I have two systems of linear equations:

For $P(x)$:

$16b + c = -458 \quad ...(1)$

$20b + c = -747 \quad ...(2)$

Subtract equation (1) from equation (2):

$(20b + c) - (16b + c) = -747 - (-458)$

$4b = -289 \Rightarrow b = -\frac{289}{4}$

Now plug $b$ back into equation (1):

$16\left(-\frac{289}{4}\right) + c = -458 \Rightarrow -1156 + c = -458 \Rightarrow c = -458 + 1156 = 698$

So $P(x) = 2x² - \frac{289}{4}x + 698$

For $Q(x)$:

$16d + e = 566 \quad ...(3)$

$20d + e = 853 \quad ...(4)$

Subtract equation (3) from equation (4):

$(20d + e) - (16d + e) = 853 - 566$

$4d = 287 \Rightarrow d = \frac{287}{4}$

Now plug $d$ back into equation (3):

$16\left(\frac{287}{4}\right) + e = 566 \Rightarrow 1148 + e = 566 \Rightarrow e = 566 -1148= -582$

So $Q(x)=-2x^{2}+\frac{287}{4}x-582$.

Now, $P(0)=c=698$.

$Q(0)=e=-582$.

Therefore, $P(0)+Q(0)=698+(-582)=116$.

Final Answer

$\boxed{116}$.
Authors
Prime Intellect Team
Share
Acknowledgements

SYNTHETIC-2 Release: Four Million Collaboratively Generated Reasoning Traces

We are releasing SYNTHETIC-2, an open dataset of four million verified reasoning traces spanning the most comprehensive set of complex reinforcement learning tasks and verifiers released to date. The dataset was collaboratively generated by compute contributors across the globe via our pipeline-parallel decentralized inference. Over 1,250 GPUs joined in 3 days — from 4090s to H200s — creating data for complex RL tasks.

July 10, 2025

SYNTHETIC-2: Planetary-Scale Pipeline Parallel Inference for Verified Reasoning

Today, we’re excited to launch SYNTHETIC-2, our next-generation, open-source reasoning dataset and planetary-scale, pipeline-parallel decentralized inference run.Built on our peer-to-peer inference stack and powered by the new DeepSeek-R1-0528 model, SYNTHETIC-2 generates verified reasoning traces spanning the most comprehensive set of complex reinforcement-learning tasks and verifiers released to date.

June 23, 2025

PCCL - Prime Collective Communications Library

We are excited to release the Prime Collective Communications Library, a low-level communication library built for decentralized training across the globe.

May 20, 2025

ESSAYS

Related Posts

SYNTHETIC-2 Release: Four Million Collaboratively Generated Reasoning Traces

We are releasing SYNTHETIC-2, an open dataset of four million verified reasoning traces spanning the most comprehensive set of complex reinforcement learning tasks and verifiers released to date. The dataset was collaboratively generated by compute contributors across the globe via our pipeline-parallel decentralized inference. Over 1,250 GPUs joined in 3 days — from 4090s to H200s — creating data for complex RL tasks.

July 10, 2025

SYNTHETIC-2: Planetary-Scale Pipeline Parallel Inference for Verified Reasoning

Today, we’re excited to launch SYNTHETIC-2, our next-generation, open-source reasoning dataset and planetary-scale, pipeline-parallel decentralized inference run.Built on our peer-to-peer inference stack and powered by the new DeepSeek-R1-0528 model, SYNTHETIC-2 generates verified reasoning traces spanning the most comprehensive set of complex reinforcement-learning tasks and verifiers released to date.

June 23, 2025

PCCL - Prime Collective Communications Library

We are excited to release the Prime Collective Communications Library, a low-level communication library built for decentralized training across the globe.

May 20, 2025